当てはまったあなたはズバリ○○でしょう!!
いきなりですが質問です。あなたは以下の項目にお心当たりはありませんか?
1. 合コンで海へ行ったのに異性には目もくれず、刺胞動物や棘皮動物といった磯のヘンな生きものと戯れてしまった
2. 気になるあのコと花火大会に行ったのに、「た~まや~~!!」の大合唱の中で一人「あ、紅色…ストロンチウムだ! 今度は藍色……インジウム!!」とマニアックな炎色反応のかけ声が止まらない
3. こっそりキムワイプを口に含み、背徳感を感じつつも恍惚とした表情で「おいしい」とつぶやいてしまった
4. 「♪世の中~すべて波だらけ~♪」と波動力学をたたえる「シュレーディンガー音頭」を暗唱できてしまう
5. 貝殻の曲線が対数螺旋の数式で描けることを知ったとき、「おお!神はこんなにも美しく世界を創りたもうた!!」と感動せずにはいられなかった
ひとつでも当てはまってしまったそこのあなた!おめでとうございます。栄誉ある「理系変態(※)」の素質を十分に備えていらっしゃいますね。
理系変態にとって最も根幹に流れる学問は数学。「突き詰めると、生物は化学になり、化学は物理になり、物理は数学になり、数学は化け物になる」という格言(?)があるとおり、数学は理系の中でも高次元に君臨しているといえるでしょう。
ということで今回は、そんな高尚な数学と身近な食材との接点にせまります。
フラクタル造形の美しさ:ロマネスコ
最初にご紹介するのはロマネスコ。カリフラワーの一種であるロマネスコは、コリコリした食感がおいしい黄緑色の蕾野菜です。最近はデパートなどに出回る機会も増えましたね。

その特徴はなんといっても精巧な造形美でしょう。螺旋状のとんがり帽子が集まったような形状をしており、そのとんがり帽子はまた小さなとんがり帽子の集合体に、その小さなとんがり帽子は…(以下略)。このように一部分が全体を縮小した形(自己相似)をしている形状をずっと繰り返しているものを「フラクタル」といいます。
さらにロマネスコの螺旋の配置は、フィボナッチ数列の要素に従っています。フィボナッチ数列とは、連続した2つの数字を足して次の数字を導き出すもの。螺旋の数は、1,1,2,3,5,8,13…(以下略)の中に現れる数字となっているので、興味のある(暇な)方はぜひ数えてみてくださいね。
伝統的な日本食材にもフラクタル:ワラビ
フラクタル形状は日本で昔から食べられてきた山菜にも見られます。ワラビやクサソテツ(コゴミ)がその例です。今ちょうど旬を迎えている地域も多いことでしょう。

シダ植物であるこれらの芽は、渦巻き模様が自己相似。季節限定のおいしさもさることながら、細部をよく見てみるとその美しさにほれぼれしてしまいますよ。葉っぱが開ききった形状も、ギザギザ図形の繰り返し(羽状複葉)になっていて素敵です。

計算モデルで模様をシミュレーション:アサリ
最後にご紹介するのはアサリ。貝殻の模様が千差万別で、ずっと眺めていても飽きません。これは遺伝子の多様性と環境への対応の掛け合わせがなせる技ですね。
こうした貝殻の模様も、古くから「セル・オートマトン」という計算モデルなどによってシミュレーションが試みられてきました[※1]。いやぁ、シミュレーション結果は本物そっくりです。
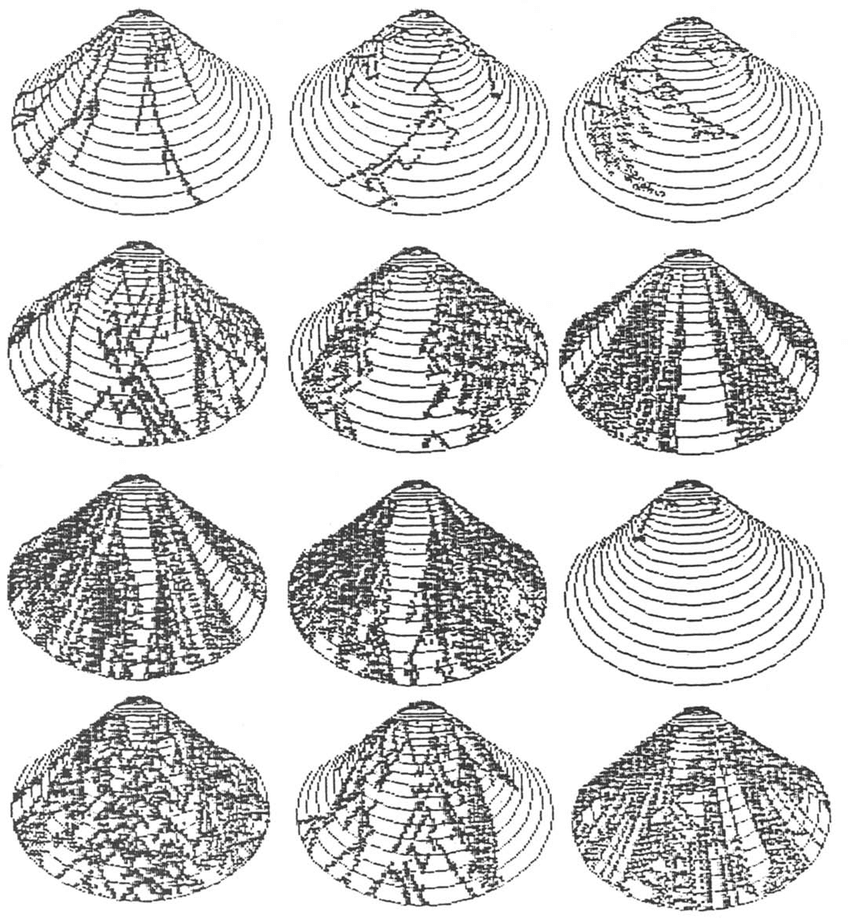
ちなみに最初の質問5でも記したとおり、貝殻の描く曲線は二枚貝であれ巻き貝であれ、「対数螺旋」という一種類の数式ですべて表現することができます。そう、アサリもシジミもハマグリもサザエもアワビもみんな……。

食材を味わう上では1ミリたりとも役に立たない知識、いかがでしたか?理系変態でないにもかかわらずここまで読み進んでくださったあなたには、心から敬意を表します。最後に言えることはただひとつ。数学好きも数学嫌いも関係なく、おいしくいただきましょう!
※理系に対する温かいリスペクトと絶妙なる悲哀の気持ちを込めた造語です。ごめんなさい。ちなみにそんな筆者自身ももちろん理系変態です、あしからず。
参考:
※1 Pigment color patterns of molluscs as an autonomous process generated by asynchronous automata






